Chapter 5 Evolutionary Mechanisms I: Modeling Selection

The Hardy-Weinberg principle we learned about in the last chapter provides a simple framework to test whether evolutionary forces are acting on a locus within a population. If a population is in Hardy-Weinberg disequilibrium at a particular locus, we know that an evolutionary force is skewing relative genotype frequencies away from what is predicted based on the allele frequencies in a population. Evolutionary forces might include selection, mutation, genetic drift, migration, or non-random mating. In this and the next chapter, we will get to know the different evolutionary forces in more detail, and we will explore how each force—and interactions between them—shapes genetic variation and allele frequencies across generations. To do so, we will use simple mathematical models to simulate allele frequency changes under different scenarios. First, we will learn how the outcome of selection varies depending on the fitness distribution among genotypes and the starting allele frequency in a population. In the next chapter, we will expand this simplified view and also include mutation, genetic drift, migration, and non-random mating in our thinking.

5.1 The Effects of Selection

Rosemary and Peter Grant’s work has shown us how natural selection can drive rapid evolution of phenotypic traits. But what are the genetic ramifications of selection? How does selection impact genetic variation and allele frequencies at a particular locus? Per definition, we know that selection favors the success of certain genotypes over others; this is one way Hardy-Weinberg disequilibrium can be generated. It is this biased success of certain genotypes that ultimately causes allele frequency changes across generations. For example, if the fitness of an individual is contingent on the number of \(A_1\) alleles at a particular locus, we would expect the \(A_1\) allele to become more common than the \(A_2\) allele through successive generations.

Such allele frequency changes across generations are well documented from evolution experiments. For example, Dawson (1970) conducted research on flour beetles (Tribolium castaneum). In his colonies, he observed a deleterious recessive mutation, where individuals with two copies of the recessive allele (l) could not survive, but heterozygotes (wt/l) and individuals that were homozygous for the wildtype (wt) allele had normal fitness. This represents a classical dominant-recessive inheritance. To test the evolutionary consequences of the deleterious recessive allele, Dawson assembled experimental populations composed solely of heterozygous individuals, which means that the allele frequencies of wt and l were both 0.5. He then let the populations evolve for several generations and measured the allele frequencies of wt and I in each generation.

As you can see in Figure 5.1, the allele frequency of wt increased in each generation. Since \(p+q=1\) for any biallelic locus, the frequency of l decreased concurrently. Hence, selection against the recessive lethal allele caused it to decline in frequency over time. This makes intuitive sense, considering the offspring of the heterozygous individuals of the initial population were 25% wt/wt, 50% heterozygous wt/l, and 25% l/l. While all the individuals with at least one wt allele survived and reproduced, individuals that were homozygous for the recessive allele perished, disproportionately removing l alleles from the population.

Figure 5.1: Selection against a deleterious recessive mutation causes significant changes in allele frequencies over short periods of time. Data from Dawson (1970).

Similar changes in allele frequencies can be observed if populations that are polymorphic at a particular locus are exposed to different environmental conditions. For example, many fruit fly (Drosophila melanogaster) populations are polymorphic at the Adh locus, which encodes alcohol dehydrogenase, the same enzyme that detoxifies ethanol in your liver after a fine glass of wine. The two alleles in fruit flies differ in the rate at which they process ethanol. One is a fast allele (Adh^f), and the other is a slow allele (Adh^s). Cavener and Clegg (1981) used populations with this polymorphism, letting different replicate populations evolve on media that contained alcohol, or in non-alcoholic control populations. While the control populations only exhibited minor fluctuations in allele frequencies across generations, the frequency of the Adh^f allele significantly increased in populations exposed to ethanol (Figure 5.2). The difference in evolutionary trajectories can be explained by the fitness benefit the Adh^f allele confers in different environments: when ethanol is present, having faster detoxification is clearly advantageous. But if there is no ethanol in the environment, individuals with any genotype will be similarly successful because there is no advantage to being able to detoxify alcohol faster or slower.

Figure 5.2: Allele frequency changes at the Adh locus in ethanol-exposed and control populations. Allele frequencies change drastically in populations that are exposed to the critical source of selection, ethanol. Data from Cavener and Clegg (1981).

Evidence for changes in allele frequencies in response to selection does not just come from laboratory experiments, but also from natural populations where time series of the genotypic composition of populations are available. One of the most amazing data sets in recent years comes from over 540 whole or partial genome sequences that were obtained from fossilized human remains—some of which are almost 14,000 years old.

This time series spans some major transitions in human evolution, including the advent of agriculture and correlated changes in human diets that occurred about 10,000 years ago. Around that time, humans also started to domesticate livestock for meat and milk production. Many of these changes represented novel sources of selection, especially the availability of milk as a dietary component past weaning and into adulthood. As much as mammals rely on milk for nutrition right after birth, this food source is not really available to any species after weaning. Accordingly, the production of lactase—the enzyme that mediates digestion of milk sugar (lactose)—stops after weaning, leaving adult mammals unable to digest lactose. Some of you may be familiar with that problem. Depending on your heritage, you may feel significant discomfort after eating dairy, because your body cannot handle the lactose (this is known as lactose intolerance).

It turns out that lactose intolerance is prevalent in human populations that do not have a cultural history of using domesticated animals for milk production. This raises the question of how lactose tolerance evolved in populations that do have a history of dairy use.

Analyses of ancient DNA indicated that alleles conferring lactose tolerance (also known as lactase persistence alleles) were virtually absent in human populations prior to the domestication of dairy animals (Figure 5.3). In European populations with a history of dairy farming, lactase persistence alleles did not start to spread until about 5,000 years ago, matching the timeline of domestication. Overall, empirical evidence from experiments and natural systems indicates that selection can have profound impacts on allele frequencies even over relatively short time frames.

Figure 5.3: Analyses of ancient DNA indicates an increase in the frequency of lactase persistence alleles starting about 5,000 years ago. Different geographic regions are color-coded and the size of markers is proportional to the number of genomes used to infer allele frequences. Data from Marciniak & Perry (2017).

5.1.1 Frequency-Dependent Selection

While evolution experiments usually create conditions where the direction and strength of selection remains constant, selection in natural populations often varies spatially or temporally. For example, fluctuating selection can be associated with environmental change, which was exemplified in Darwin’s finches, whose beaks can evolve to be larger or smaller depending on the available food resources. A special case of fluctuating selection is frequency-dependent selection, where the fitness of a genotype depends on the genotypic composition of the population. We distinguish two types of frequency-dependency: positive and negative.

In positive frequency-dependent selection, the fitness of a genotype increases as it becomes more common in a population, and consequently, selection rapidly drives common alleles to fixation. Positive frequency-dependent selection plays a major role in the evolution of signaling traits, where the efficiency of a signal is dependent on the frequency of its use. Notable examples include the evolution of social signals, flower coloration for pollinator attraction, and warning signals that indicate danger or unpalatability.

Positive frequency-dependent selection

A great example of positive frequency-dependent selection includes selection on warning signals in toxic South American butterflies of the genus Heliconius. Some Heliconius species exhibit extensive geographic variation in their warning colors, but different species in the same geographic region are often strikingly similar (Figure 5.4). This is because different species in the same region mimic each other, developing shared signals to deter predators. Similar signals mean that predators are more likely to recognize the pattern of unpalatability. This is similar to the independent evolution of yellow and black stripes in wasps, bees, and many other insects that signal danger.

Figure 5.4: Mimicry in Heliconius butterflies. Specimens in the same row belong to the same species (top: H. melpomene; bottom: H. erato). Specimens in the same column were collected in the same geographic region. Image from Meyer (2006), CC BY 2.5, via Wikimedia Commons

Chouteau et al. (2016) tested whether positive frequency-dependent selection could explain the evolution of mimicry in Heliconius butterflies. They used prey models and placed them in different Heliconius populations that varied in the relative frequencies of different warning colorations, predicting that the rate of predation would be low if models matched the common warning phenotype. Indeed, models that resembled rare morphs were much more likely to be attacked by predators than models that resembled the common morph (Figure 5.5). In other words, the more common a particular morph is, the less likely it is to succumb to a predator, and consequently, it will have a higher fitness compared to the rarer morphs. Over the course of multiple generations, such positive frequency dependent selection can generate the evolution of coordinated warning signals across species inhabiting the same region.

Figure 5.5: Positive frequency dependent selection. Data from Chouteau et al. (2016).

Negative frequency-dependent selection

In negative frequency-dependent selection, the fitness of a genotype declines as it becomes more common. Negative frequency-dependency is a mechanism by which genetic variation is maintained in a population, and it can be an important evolutionary force acting on a wide variety of traits. Perhaps most well-known is how negative frequency-dependence shapes the evolution of many traits associated with host-pathogen interactions. As certain host defense strategies become more common, pathogens rapidly evolve to adapt to those defenses. As a consequence, individuals with more common defense strategies exhibit lower fitness than rare ones, leading to fluctuations in genotype frequencies over time.

Another great example of negative frequency-dependent selection comes from the orchid Dactylorhiza sambucina, which exhibits a striking polymorphism in flower coloration (Figure 5.6). While many plant communities are subject to positive frequency-dependent selection to coordinate signals for pollinator attraction, Dactylorhiza cheats: unlike most flowers, those of Dactylorhiza do not provide any rewards to pollinators in the form of nectar. As a consequence, pollinators learn to avoid Dactylorhiza flowers.

Figure 5.6: Dactylorhiza sambucina (yellow and purple/red forms growing together) in Andorra. Photo by Strobilomyces, CC BY-SA 3.0, via Wikimedia Commons.

Dactylorhiza’s counter-adaptation to this learned avoidance is a flower color polymorphism, which is thought to be maintained by negative frequency-dependent selection. The idea is that if one color morph gets too abundant and pollinators start avoiding it, then pollinators simply switch to the rarer color morph that they do not yet associate with a lack of reward. If this is correct, the fitness of a color morph should decline with its frequency. Gigord et al. (2001) tested this idea by conducting an experiment where they varied the relative frequency of different color morphs and quantified reproductive success. As predicted, male reproductive success was negatively correlated with relative frequency of the morph (Figure 5.7), indicating a rare morph advantage that is characteristic for negative frequency-dependent selection.

Figure 5.7: As predicted by negative frequency-dependent selection, reproductive success in Dactylorhiza color morphs is negatively correlated with the frequency of the morph in the population. Data from Gigord et al. (2001).

5.2 Modeling the Effects of Selection

While the consequences of selection in terms of changing allele frequencies may seem trivial at first sight, the exact outcome of selection actually depends on a number of parameters, including the starting allele frequency and the fitness distribution across different genotypes. To develop a nuanced understanding of alternative evolutionary outcomes in response to selection, we will use simple mathematical models to explore how different starting conditions shape evolutionary trajectories. Here, I provide some conceptual background on how these mathematical models work. Later, you will learn how you can easily run different models in R.

5.2.1 Relative Fitness

Modeling changes in allele frequencies in response to selection requires a modification of the formulas associated with the Hardy-Weinberg principle. When calculating allele frequencies across generations, we have to take into account fitness differences between the genotypes. While fitness is typically measured through a variety of proxies in natural populations (e.g., survival, reproductive success, growth, etc.), having species- or even study-specific metrics for fitness is not conducive to mathematical modeling. So, rather than considering different fitness components, we can just subsume different metrics into a single, idealized measure of fitness, which is called relative fitness. Relative fitness expresses the fitness of different genotypes relative to each other, and it can be any positive number, including zero. In this class, we will select the genotype with the highest fitness and set its relative fitness to 1 (representing the highest or 100 % fitness). The fitness of other genotypes can then be expressed in relative to the highest fitness, 1.

The difference in relative fitness between genotypes is called the selection coefficient, \(s\), indicating how fitness and selection are directly related to each other. Table 5.1 provides a practical example for the description of relative fitness using a biallelic locus with dominant-recessive or other modes of inheritance. The dominant phenotype has the highest fitness (1), and the fitness of the other genotypes is expressed in relation to that. Note that the mean (average) fitness, \(\bar{w}\), can be calculated as:

\[\begin{equation} \bar{w} = fr(A_1A_1)(w_{11})+fr(A_1A_2)(w_{12})+fr(A_2A_2)(w_{22}) \tag{5.1} \end{equation}\]

Table 5.1: Example of relative fitness descriptions for a dominant-recessive inheritance (w₁₁=w₁₂) and other modes of inheritance. Note that the A₁A₁ genotype has the highest relative fitness (w₁₁=1). Description of relative fitness in the former case requires a single selection coefficient, because the phenotype of A₁A₁ and A₁A₂ are by definition the same. For other modes of inheritance (e.g., additive, heterozygote advantage, or disadvantage), two selection coefficients are necessary to describe the fitness distribution of genotypes relative to w₁₁.

	AA	Aa	aa
Dominant-recessive inheritance	1.0 .	1.0 .	0.8 s=0.2
Other modes of inheritance	1.0 .	0.8 s1=0.2	0.6 s2=0.4

5.2.2 Calculating Allele Frequency Changes

Based on relative fitness, we can calculate the allele frequency of the next generation as a function of allele frequencies in the current generation. Just take a look at the modified Punnett square from the previous chapter for a graphical representation. In the absence of selection or any other evolutionary forces (i.e., under Hardy-Weinberg assumptions), the genotype frequencies of the next generation are defined as:

\[\begin{align} fr({A_1A_1}')=p^2 \tag{5.2}\\ fr({A_1A_2}')=2pq \tag{5.3}\\ fr({A_2A_2}')=q^2 \tag{5.4} \end{align}\]

If the \(A_1A_1\) genotype has the highest fitness (w₁₁=1), we can then adjust the frequency of genotypes after selection by factoring in the fitness differences between AA and Aa relative to aa. Assuming a dominant-recessive inheritance, this means:

\[\begin{align} fr({A_1A_1}')=fr({A_1A_1}) \tag{5.5}\\ fr({A_1A_2}')=fr({A_1A_2}) \tag{5.6}\\ fr({A_2A_2}')=fr({A_2A_2})(1-s) \tag{5.7} \end{align}\]

Similarly, the allele frequencies of the next generation (p_n+1 and q_n+1) can then be calculated directly from the allele frequencies of the current generation (p_n and q_n):

\[\begin{align} p_{n+1}=\frac{fr({A_1A_1})+\frac{1}{2}fr({A_1A_2})}{fr({A_1A_1})+fr({A_1A_2})+fr({A_2A_2})(1-s)}=\frac{fr({A_1A_1})+\frac{1}{2}fr({A_1A_2})}{w̄} \tag{5.8}\\ q_{n+1}=\frac{\frac{1}{2}fr({A_1A_2})+fr(A_2A_2)(1-s)}{fr({A_1A_1})+fr({A_1A_2})+fr({A_2A_2})(1-s)}=\frac{\frac{1}{2}fr({A_1A_2})+fr(A_2A_2)(1-s)}{w̄} \tag{5.9} \end{align}\]

The mathematical formula for other modes of inheritance is the same, except that we need to use different selection coefficients.

These simple equations underlie the majority of models you will run during the R exercise associated with this chapter. If you are thinking “Errrr, what? Simple?”, don’t worry too much! These formulas are already integrated into R functions that will automatically calculate allele frequency changes across many generations based on a few input parameters. The math provided here is just to help you understand how these algorithms actually work.

5.3 Case Study: Modeling Selection

The key goal of this case study is for you to learn how to model the effects of selection in R and apply that knowledge to systematically explore evolutionary outcomes by manipulating key input parameters. All models of selection require you to input a starting allele frequency (p₀) for the initial generation, the number of generations (time) you want the model to run for, and—perhaps most importantly—the distribution of fitness among the different genotypes. For simplicity, all of our models assume a biallelic locus in a diploid organism.

Since selection is blind to the genotype and can only act on phenotypic traits, it is important to consider different modes of inheritance when studying the possible outcomes of selection. While it is often assumed that most traits exhibit a dominant-recessive inheritance, this is not actually true. Hence, we will consider a number of scenarios beyond dominant-recessive inheritance to explore how selection actually impacts evolutionary outcomes:

1. We will contrast evolutionary outcomes when selection acts for (Figure 5.8-A) or against (Figure 5.8-B) dominant phenotypes, assuming dominant-recessive inheritance (w₁₁=w₁₂).

2. We will explore evolutionary outcomes when alternative alleles have additive effects, such as when the fitness of heterozygotes is intermediate between the fitness of the homozygotes (w₁₁ > w₁₂ > w₂₂ or w₁₁ < w₁₂ < w₂₂; Figure 5.8-C).

3. Sometimes heterozygotes will have a fitness advantage over both homozygous genotypes. We will consider cases where there are no fitness differences between the two homozygous genotypes (w₁₁ = w₂₂; Figure 5.8-D) and where the fitness of the homozygous genotypes differ (w₁₁ ≠ w₂₂; Figure 5.8-E).

4. Sometimes heterozygotes will have a fitness disadvantage over both homozygous genotypes. We will again consider cases where there are no fitness differences between the two homozygous genotypes (w₁₁ = w₂₂; Figure 5.8-F) and where the fitness of the homozygous genotypes differ (w₁₁ ≠ w₂₂; Figure 5.8-G).

   Note: you may ignore the panel labeled H.

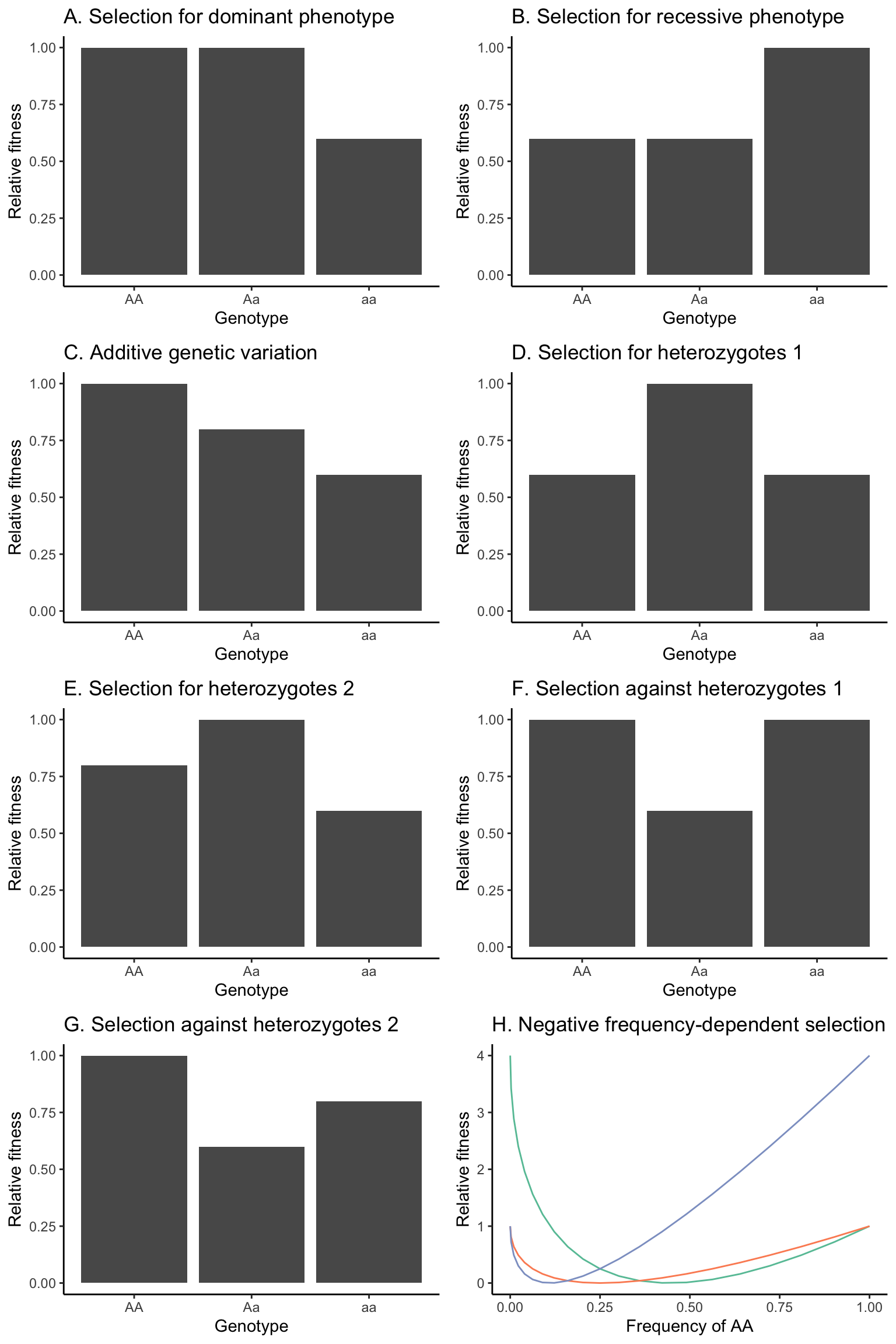
Figure 5.8: Hypothetical fitness distributions among genotypes that will be used in different scenarios to model the outcomes of selection. (A) Selection for the dominant phenotype, assuming a dominant-recessive inheritance. (B) Selection for the recessive phenotype, assuming a dominant-recessive inheritance. (C) Fitness distribution assuming a strictly additive inheritance. Note that the fitness of AA and aa could also be swapped in this scenario. (D) Selection for heterozygotes, with homozygous genotypes having equal fitness. (E) Selection for heterozygotes, with homozygous genotypes having unequal fitness. Note that the fitness of AA and aa could also be swapped in this scenario. (F) Selection against heterozygotes, with homozygous genotypes having equal fitness. (G) Selection against heterozygotes, with homozygous genotypes having unequal fitness. Note that the fitness of AA and aa could also be swapped in this scenario.

5.4 References

• Cavener DR, MT Clegg (1981). Multigenic response to ethanol in Drosophila melanogaster. Evolution 35, 1–10.

• Chouteau M, M Arias, M Joron (2016). Warning signals are under positive frequency-dependent selection in nature. Proceedings of the National Academy of Sciences USA 113, 2164–2169.

• Dawson PS (1970). Linkage and the elimination of deleterious mutant genes from experimental populations. Genetica 41, 147–169.

• Gigord LD, MR Macnair, A Smithson (2001). Negative frequency-dependent selection maintains a dramatic flower color polymorphism in the rewardless orchid Dactylorhiza sambucina (L.) Soo. Proceedings of the National Academy of Sciences USA 98, 6253–6255.

• Marciniak S, GH Perry (2017). Harnessing ancient genomes to study the history of human adaptation. Nature Reviews Genetics 18, 659–674.

• Meyer A (2006). Repeating patterns of mimicry. PLoS Biology 4, e341.

• Rice SH (2004). Evolutionary Theory: Mathematical & Conceptual Foundations. Sinauer Associates.